|
Sudoku-Help-Plus Worked Example 2
|
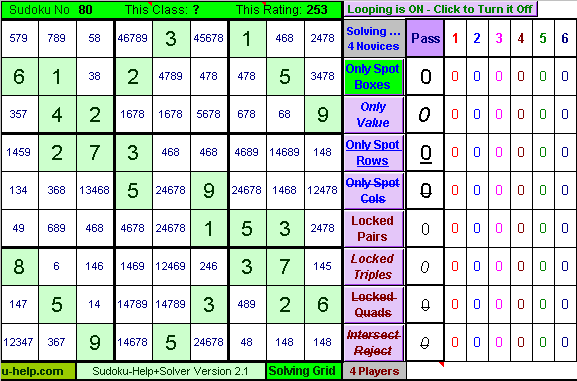
Sudoku-Help+ Puzzle No 80 (which appeared in mX as Puzzle No 207) is deceptively complex. It has 26 given values and 29 cells whose values can be immediately placed with the Only-Spot-Boxes solving rule. But after that you are stuck and to unlock the whole puzzle and solve it with pure logic requires the joint application of several different Player and Expert class elimination techniques.
To get most value out of this tutorial in solving Sudoku it is strongly recommended that you attempt to solve the puzzle independently yourself first.
This Puzzle highlights the application of the Player Class solving rule, "Intersect-Reject", as well as the "Single-Value-Chains" and "Multi-Value-Chains" Expert Class solving rules. I hope you find this tutorial instructive.
Regards Greg Shalless |
|
Sudoku-Help+ - Novice Class Rules - Only Spot Boxes:
I well not dwell on the details of the cells solved by this rule because the primary purpose of this tutorial is to focus on some of the Player and Expert Class Elimination strategies.
Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
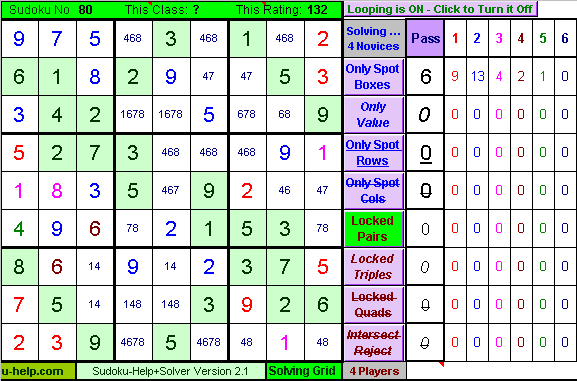
Sudoku-Help+ - Player Class Rules - Locked Pairs:
The {48} Locked Pair in the Bottom-Right Box prevents other cells in Row 9 from taking either of these values. Unfortunately it doesn't lead to further solved cells. Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
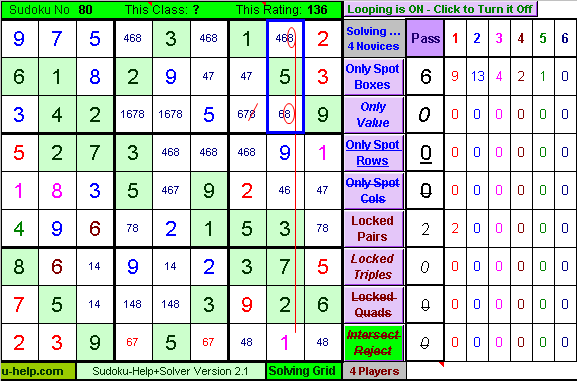
Sudoku-Help+ - Player Class Rules - Intersect Reject:
The Blue Rectangle shows the 3-cell Intersection of the Top-Right Box with Column 8. You will note that the only spots the value 8 (encircled in Red) can go in Column 8 are within this Intersection. If 8 were to be placed outside this Intersection in the Top-Right Box we would not be able to solve Column 8, so 8 can be eliminated from all such cells. However we still can't solve any new cells. By the way the Intersect-Reject Rule would have also done the same eliminations as the Locked-Pair Rule above. We are not done with this rule yet, as it comes in pretty handy again later on.
Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
As an aside, to further clarify what I mean by the 3-cell Intersection between a Box and a Row or Column I present the diagram on the right. The Pink Cells represent a Row where the Mauve Cells are the 3-cell Intersection between that Row and one of the Blue boxes. The Yellow Cells represent a Column where the Green cells are the 3-cell Intersection between that Column and the other Blue box. (The Orange cell is the Intersection between the Row and the Column).
The Intersect-Reject rule effectively says this: If a Value in the Row is confined to the Mauve cells, it can't go in the Blue cells or you won't be able to place it in the Row. Similarly if a Value in the Box is confined to the Mauve cells, it can't go in the Pink (or the Orange) cells or you won't be able to place it in the Box. If a Value in the Column is confined to the Green cells, it can't go in the Blue cells or you won't be able to place it in the Column. Similarly if a Value in the Box is confined to the Green cells, it can't go in the Yellow (or the Orange) cells or you won't be able to place it in the Box.
Now back to our puzzle.
|
 |
|
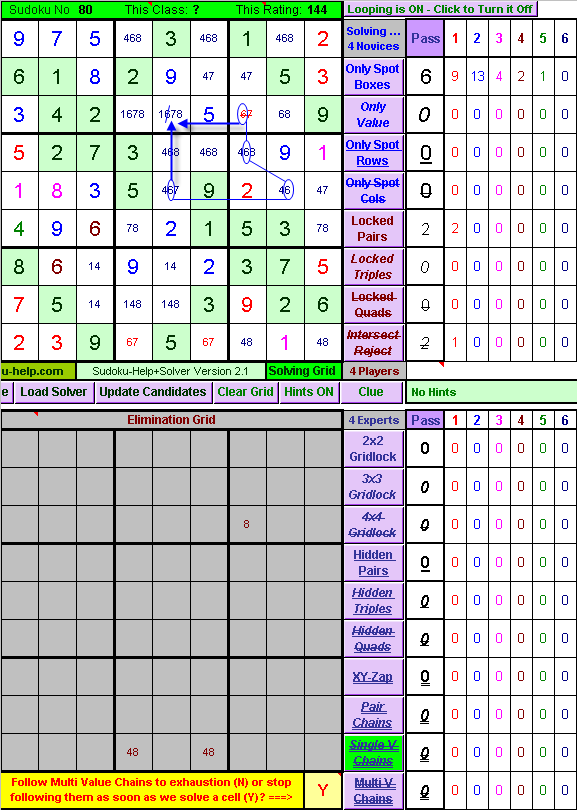
Sudoku-Help+- Expert Class Rules - Single Value Chains:
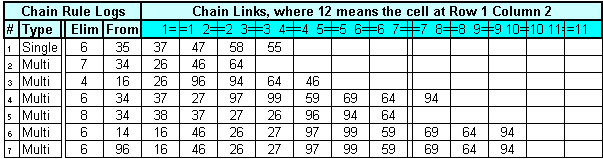
One link in a Single-Value-Chain is two cells in the same Constraint Region (my generic term for a Row, Column or Box), which are the only spots in that Constraint Region that a particular Value can go. A two-link chain is formed when two such links on the same particular Value have a cell in common. In each such link one end is the value, the other isn't, but we don't know which yet. In any odd length Single-Value-Chain one of the end-points must be the value and the other cannot be. In this puzzle we have a 3-link Single-Value-Chain on the value 6, where each link is shown by two blue circles joined by a blue line. You will note that there are only 2 spots 6 can go in Column 7 (1st link in the Chain), only 2 spots it can go in the Middle Right Box (2nd link) and only 2 spots it can go in Row 5 (3rd link). The cell at Row 3 Column 5 is in the same Row as one of the end-points of this Chain and the same Column as the other, and since we know that one of those two end-points must be 6, the cell at Row 3 Column 5 cannot be 6. But we still can't solve any more cells!
Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
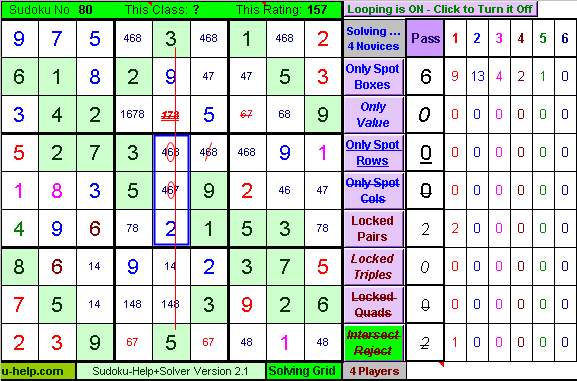
Sudoku-Help+ - Player Class Rules - Intersect Reject:
The Blue Rectangle shows the 3-cell Intersection of the Central Box with Column 5. You will note that (thanks to the 6 eliminated in the previous step by the Single-Value-Chain) the only spots the value 6 (encircled in Red) can go in Column 5 are within this Intersection. If 6 were to be placed outside this Intersection in the Central Box we would not be able to solve Column 5, so 6 can be eliminated from all such cells. However we still can't solve any new cells.
Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
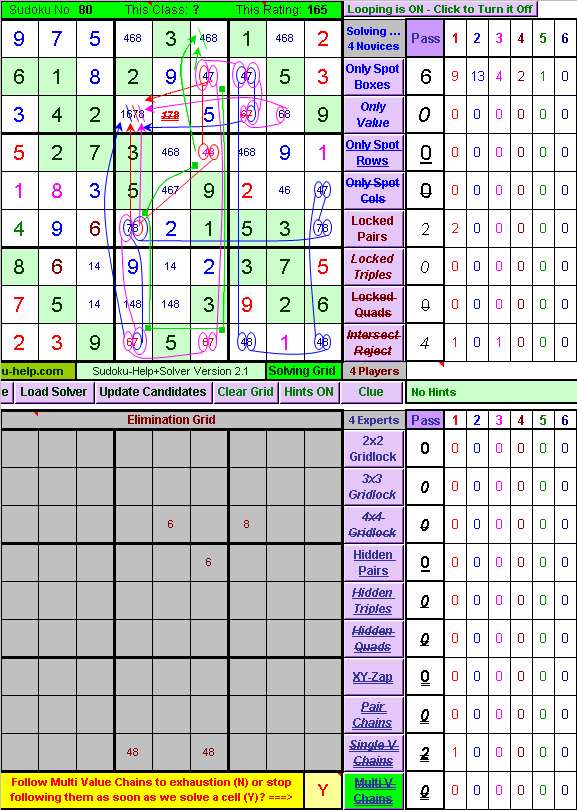
Sudoku-Help+ - Expert Class Rules - Multi Value Chains:
The work done previously has set up a number of additional bi-value (with only 2 possible values) cells which gives us the opportunity to deploy the Multi-Value-Chains rule. There are 4 Multi-Value-Chains shown in the image below and 3 of them serve to eliminate 3 different values from the cell at Row 3 Column 4, such that there is only one option left and that cell is thereby solved. The first and simplest Chain to follow is shown in Red and eliminates 7 from that cell. It is a two-link Chain and is otherwise known as the XY-Zap rule. 6 gets eliminated from the cell at Row 3 Column 4 by the 7-link Multi-Value-Chain shown in Blue. And finally 8 gets eliminated from that cell by the 6-link Chain shown in Pink. Now there is another Multi-Value-Chain there that eliminates 4 from the cell at Row 1 Column 6, where the two end-points of that Chain are actually in the same column. This is a 4-link Chain but because it involved a number of cells that already have multiple circles around them I decided to highlight it in a slightly different way using a Green box in the corner of each cell involved in the Chain. There may well be other Multi-Value-Chains present but because the Solver is operating in a mode where it stops as soon as it finds a solved cell (in the hope that this is enough to solve the puzzle) we will stop looking as well and see how far the solved cell takes us. Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
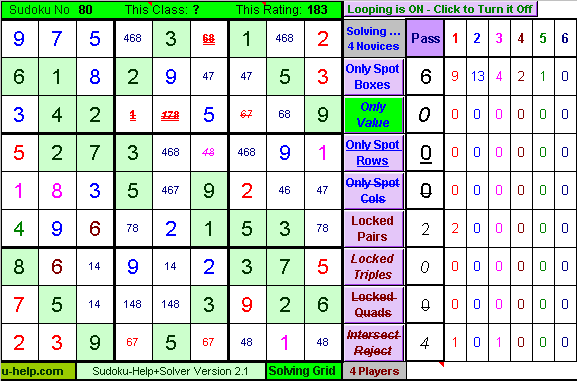
Finally some real progress, we can now solve a cell, which we will do with the Only-Value rule. The trouble is that's as far as we can go, but it does set up a couple more bi-value cells, so maybe Multi-Value-Chains will come to our rescue, again! Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
 |
|
Sudoku-Help+ - Expert Class Rules - Multi Value Chains (again):
A new 5-link Multi-Value-Chain is shown in Blue which enables us to eliminate 6 as a candidate in the cells at Row 1 Column 4, and also at Row 9 Column 6, the latter of which solves that cell. So once again although there may be other Multi-Value-Chains present, we stop looking for more and see how far we can go with the new information. Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
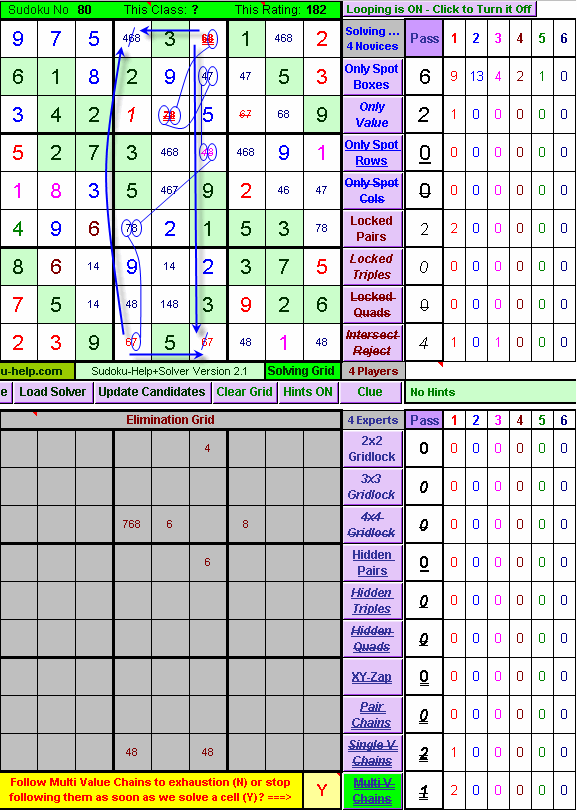 |
|
From here it turns out that the puzzle is now a piece of cake to solve completely. I chose to do it with the Novice Class rule Only-Spot-Cols. Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
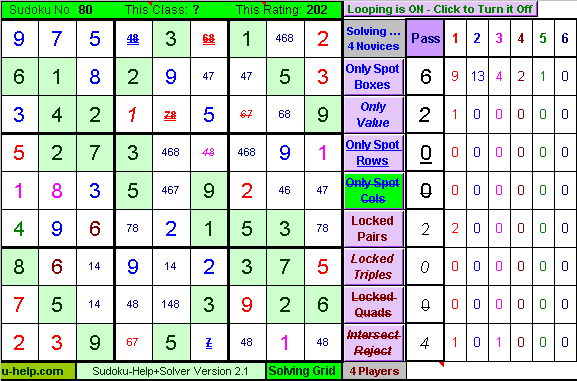 |
|
Sudoku-Help+ - Expert Class Rules - XY-Zap:
As was suggested there were other Multi-Value-Chains present at that final step that unlocked the puzzle, and some of them were considerably easier to find than the one we showed you, which was the first one the Sudoku-Help+Solver happened to find. However had we used the XY-Zap rule instead, we would have found a number of 2-link Multi-Value-Chains, which is after all what the XY-Zap rule really is. Each one is shown in a different colour. Move the Mouse Over the picture to see what Sudoku-Help+Solver does. |
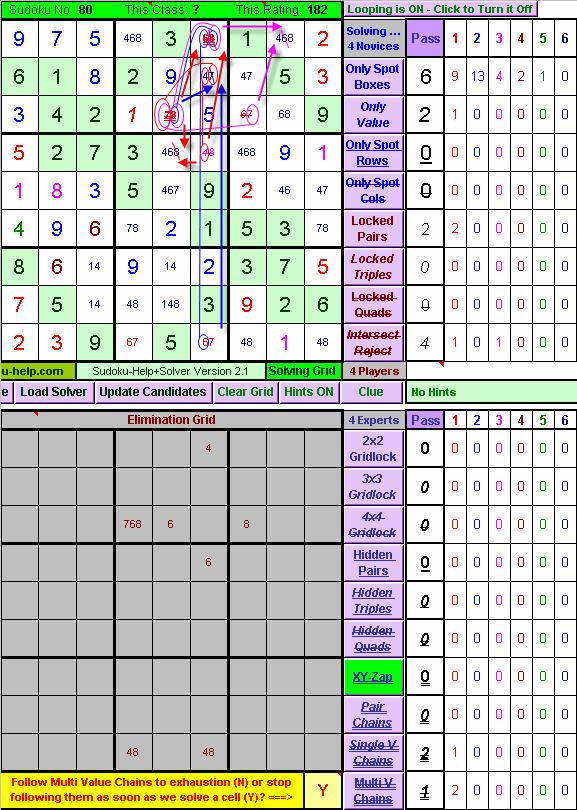 |